 |
5. Diverses autres notions MATLAB/Octave |
 |
|
5. Diverses autres notions MATLAB/Octave |
|
 10:23 min |
La gestion du temps est un chapitre important en programmation. Beaucoup de données se réfèrent au temps (dates et/ou heures), celui-ci constituant souvent la 4e dimension (après l'espace 3D), par exemple pour des séries temporelles (hydro-météorologiques, bio-chimiques...).
Cette vidéo présente la forme sous laquelle on stocke des dates et des heures, et comment on les affiche de façon lisible. La solution sous MATLAB/Octave est analogue à d'autres logiciels (tels que les tableurs...), les dates et heures n'étant rien d'autre que des nombres réels formatés de manière particulière. Nous complétons cette vidéo par la présentation de quelques fonctions utiles de "timing", c-à-d. permettant de déterminer le temps d'exécution d'un programme ou d'un morceau de code. |
De façon interne, MATLAB/Octave gère les dates et le temps sous forme de nombres (comme la plupart des autres langages de programmation, tableurs...). L' "origine du temps", pour MATLAB/Octave, a été définie au 1er janvier de l'an 0 à 0h, et elle est mise en correspondance avec le nombre 1 (vous pouvez vérifier cela avec datestr(1.0001)). Chaque jour qui passe, ce nombre est incrémenté de 1, et les heures, minutes et secondes dans la journée correspondent donc à des fractions de jour (partie décimale du nombre exprimant le temps).
On obtient la liste des fonctions relatives à la gestion du temps avec 
helpwin timefun ou au chapitre "Timing Utilities" du manuel Octave.
| Fonction | Description |
 date_string = date
|
Retourne la date courante sous forme de chaîne de caractère au format 'dd-mmm-yyyy' (où mmm est le nom du mois en anglais abrégé aux 3 premiers caractères)
Ex: date retourne 08-Apr-2005 |
|
a) date_num = now b) date_num = today [M: financial] [O: financial] |
Retourne le nombre exprimant : a) la date et heure locale courante (donc le nombre de jours et fractions de jours écoulés depuis le 1er janvier 0000) b) la date courante (donc le nombre de jours écoulés depuis le 1er janvier 0000)
Ex: |
| date_vec = clock |
Retourne la date et heure courante sous forme d'un vecteur-ligne date_vec de 6 valeurs numériques [annee mois jour heure minute seconde]. Est identique à datevec(now). Pour avoir des valeurs entières, faire fix(clock). Ex: clock retourne le vecteur [2005 4 8 20 45 3] qui signifie 8 Avril 2005 à 20h 45' 03" |
| Fonction | Description |
|
date_string =
a) datestr(date_num {,'format'})
b) datestr(date_vec {,'format'})
c) datestr(date_string {,'format'}) |
Convertit en chaîne de caractères la date et heure spécifiée par : a) la date numérique date_num b) le vecteur date_vec c) la chaîne date_string ; permet ainsi de reformater différemment une date exprimée sous forme de chaîne
Le formatage peut être défini par un format ou un code (voir help datestr pour plus de détails). Si le paramètre date_num est compris entre 0 et 1, cette fonction retourne des heures/minutes/secondes.
Ex: |
|
date_num = a) datenum(date_string {,'format'})
b) datenum(date_vec) |
Retourne le nombre exprimant la date et heure spécifiée par : a) la chaîne date_string ; il peut être nécessaire d'indiquer le format pour aider au décodage de la chaîne (voir second exemple ci-dessous) b) le vecteur date_vec c) les nombres annee, no_mois, no_jour, { heure, min et sec }
Ex : |
|
date_vec = ou [annee no_mois no_jour heure min sec] = a) datevec(date_string {,'format'}) b) datevec(date_nun) |
Retourne un vecteur ligne de 6 valeurs numériques définissant l'annee, no_mois, no_jour, heure, min et sec à partir de : a) la chaîne date_string ; il peut être nécessaire d'indiquer le format pour aider au décodage de la chaîne (voir second exemple ci-dessous) b) la date numérique date_num Pour avoir des valeurs entières, faire fix(datevec(date)).
Ex: |
|
Les fonctions ci-dessous sont propres à la toolbox [M: financial] et au package [O: financial]
annee = year(date_num | date_string) |
Pour la date spécifiée sous forme numérique ou chaîne, retourne respectivement l'annee, le no_mois, le no_jour, l'heure, les minutes ou les secondes. |
| Fonction | Description |
|
calendar calendar(annee, mois) calendar(date_num | date_string) mat = calendar(...) |
Affiche le calendrier du mois courant, ou du mois contenant la date spécifiée (sous forme de chaîne de caractère ou de nombre), ou du mois/annee spécifié (sous forme de nombres)
Affectée à une variable, cette fonction retourne une matrice mat 6x7 contenant les numéros de jour du mois correspondant. Ex: calendar(2005,4) ou calendar('8-Apr-2005') affichent :
Apr 2005
S M Tu W Th F S
0 0 0 0 0 1 2
3 4 5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23
24 25 26 27 28 29 30
0 0 0 0 0 0 0
(les 2 premières lignes, ici en gras, ne se trouvent pas dans la matrice 6x7 si vous appelez cette fonction calendar en l'affectant à une variable)
|
|
[numero_jour nom_jour] = weekday(date_num | date_string) |
Retourne le numero_jour (nombre) et nom_jour (chaîne) (respectivement: 1 et Sun, 2 etMon, 3 et Tue, 4 et Wed, 5 et Thu, 6 et Fri, 7 et Sat) correspondant à la date spécifiée (passée sous forme de chaîne date_string, ou de nombre date_num). Si cette fonction est affectée à une seule variable, retourne le numero_jour. Voir aussi, plus haut, la fonction datestr avec le format 'ddd'. Ex: [no nom]=weekday(732410.8646180555) et [no nom]=weekday('08-Apr-2005 20:45:03') retournent les variables No=6 et Nom='Fri' |
| weeknum(date_num | date_string) [M: financial] [O: financial] | Retourne le numéro de la semaine correspondant à la date spécifiée |
| eomday(annee, mois) |
Retourne le nombre de jours du mois/annee (spécifié par des nombres)
Ex: eomday(2005,4) retourne 30 (i.e. il y a 30 jours dans le mois d'avril 2005) |
| yeardays(annee) [M: financial] [O: financial] | Retourne le nombre de jour de l'annee spécifiée |
 easter(annee) [O: financial]
|
Retourne la date de Pâques (selon calendrier géorgien) de l'annee spécifiée |
| datetick('x|y|z',format) |
Sur l'axe spécifié (x, y ou z) d'un graphique, remplace au niveau des labels correspondants aux lignes de quadrillage (tick lines), les valeurs numériques par des dates au format indiqué Sous Octave, implémenté depuis la version 3.2.0 |
| etime(t2,t1) |
Retourne le temps en secondes séparant l'instant t1 de l'instant t2, ces 2 paramètres devant être au format clock, c-à-d. vecteurs-ligne [annee mois jour heure minute seconde].
Ex: la séquence d'instructions suivantes détermine le temps nécessaire pour générer une matrice aléatoire de dimension 1000x1000 et l'inverser : t1 = clock; A=rand(1000,1000); B=inv(A); dt = etime(clock,t1) |
| Fonction | Description |
|
pause(secondes)
pause |
Se met en attente durant le nombre de secondes spécifié.
Passée sans paramètre, la fonction pause attend que l'utilisateur frappe n'importe quelle touche au clavier.
Ex: dans un script, les lignes suivantes permettent de faire une pause explicite : |
| cputime |
Retourne le nombre de secondes de processeur consommées par MATLAB/Octave depuis le début de la session ("CPU time"). Sous Octave cette fonction a encore d'autres paramètres de sortie (voir help cputime)
Ex: t0 = cputime; A=rand(1000,1000); B=inv(A); dt = cputime-t0 : génération d'une matrice aléatoire A de dimension 1000 x 1000, inversion de celle-ci sur B, puis affichage du temps comsommé au niveau CPU pour faire tout cela (env. 8 secondes sur un Pentium 4 à 2.0 GHz, que ce soit sous MATLAB ou Octave) |
tic instructions MATLAB/Octave... ellapse_time = toc |
La fonction tic démarre un chronomètre, et la fonction toc nous retourne (sur la variable ellapse_time spécifiée) le temps écoulé en secondes depuis le démarrage du chronomètre. Notez bien que le "temps écoulé" n'est pas le "temps consommé par le CPU", et que toc n'arrête pas le chronomètre (c'est tic qui le fait). Ex: l'exemple ci-dessus pourrait être aussi implémenté ainsi : tic; A=rand(1000,1000); B=inv(A); dt = toc |
Les fonctions fzero('fonction',x0) ou fsolve('fonction',x0) permettent de trouver, par approximations successives en partant d'une valeur donnée x=x0, la(les) racine(s) d'une fonction non linéaire y=f(x), c'est-à-dire les valeurs x1, x2, x3... pour lesquelles f(x)=0 .
Remarque : sous MATLAB, la fonction fzero est standard, mais la fonction fsolve est implémentée dans la toolbox "Optimisation".
Illustrons l'usage de cette fonction par un exemple :
| Étape | Réalisation |
|
1) Soit la fonction de 3e degré : y = - 0.5*x^3 - x^2 + 15*x - 8 |
On doit donc trouver les solutions x1, x2... pour f(x)=0, donc : - 0.5*x^3 - x^2 + 15*x - 8 = 0 |
|
2) Commençons par définir cette équation sous forme d'une fonction MATLAB/Octave
(voir chapitre "Fonctions") |
Réaliser le M-file appelé fct_deg3.m contenant par conséquent le code suivant :
function [Y]=fct_deg3(X) Y = - 0.5 * X.^3 - X.^2 + 15*X - 8 return |
|
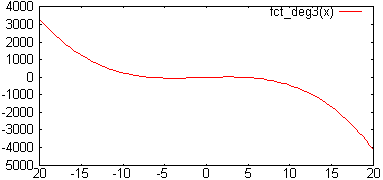
3) Puis graphons rapidement cette fonction (autour de -20 ≤ x ≤ 20) pour estimer graphiquement une valeur approximative x0 de départ
(voir l'usage de la fonction fplot au chapitre "Graphiques 2D") |
Le code fplot('fct_deg3(x)',[-20 20]) produit le graphique ci-dessous :
 |
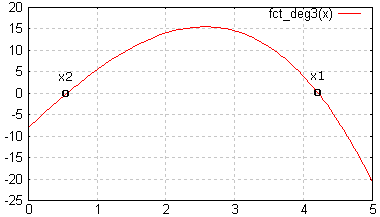
| 4) Zoomons autour de la solution (qui a l'air de se trouver vers 1 et 4) en rétrécissant l'intevalle à 0 ≤ x ≤ 5 |
Le code fplot('fct_deg3(x)',[0 5]) ; grid('on') produit le graphique ci-dessous (sauf les étiquettes x1 et x2 que nous avons ajoutées manuellement) :
 |
| 5) Choisissons la valeur de départ x0 = 5, et recherchons la première solution |
Entrons x1=fzero('fct_deg3',5) ou x1=fsolve('fct_deg3',5) Après une série d'itérations, Octave retourne : x1 = 4.2158 On peut vérifier que c'est bien une solution en entrant fct_deg3(x1) qui retourne bien 0 (ou une valeur infiniment petite) |
| 6) Choisissons la valeur de départ x0 = 0, et recherchons la seconde solution |
Entrons x2=fzero('fct_deg3',0) ou x2=fsolve('fct_deg3',0) Après une série d'itérations, Octave retourne : x2 = 0.56011 On peut vérifier que c'est bien une solution en entrant fct_deg3(x2) qui retourne bien 0 (ou une valeur infiniment petite) |
